- Livre d'or: Pour signer le livre d'or, cliquer sur "Écrire un nouveau message"
- Newsletter: Pour vous abonner et recevoir par mail un aperçu de toutes les nouvelles publications sur le site
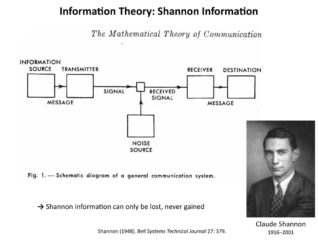
Claude Elwood Shannon
 est né en 1916 à Gaylord dans le Michigan. Alors étudiant au Massachusetts Institute of Technology (MIT), il met au point des circuits à relais électriques où un relais ouvert est représenté par 1 et un relais fermé par 0, et invente en même temps le terme « binary digit’, ou « bit », qui devient l’unité d’information. Il est l’inventeur du langage binaire qui a révolutionné l’informatique.
est né en 1916 à Gaylord dans le Michigan. Alors étudiant au Massachusetts Institute of Technology (MIT), il met au point des circuits à relais électriques où un relais ouvert est représenté par 1 et un relais fermé par 0, et invente en même temps le terme « binary digit’, ou « bit », qui devient l’unité d’information. Il est l’inventeur du langage binaire qui a révolutionné l’informatique.
En 1942, Shannon entre chez Bell. Avec son collègue Norbert Wiener, il y développe une théorie selon laquelle toute information est une quantité mesurable indépendamment de son contenu. Il publie en 1948 sa Théorie mathématique de la communication.
Théorème de Nyquist-Shannon:
Pour numériser un signal, la fréquence d’échantillonnage (sampling rate) doit être suffisamment grande pour restituer intégralement le signal.
Plusieurs étapes sont nécessaires: l’échantillonnage, puis la conversion elle-même, appelé codage.
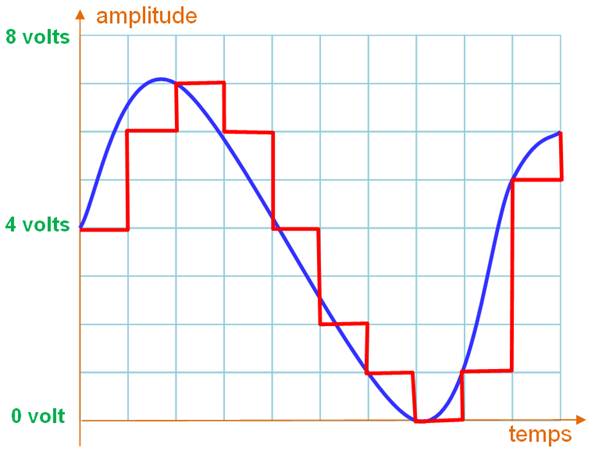
![]() Échantillonnage: Cette étape consiste à hacher le signal analogique en petites tranches temporelles selon une période bien définie par une horloge. L’amplitude (A) du signal au moment du top de l’horloge est prise comme référence pour cette tranche. C’est cette valeur qui sera codée.
Échantillonnage: Cette étape consiste à hacher le signal analogique en petites tranches temporelles selon une période bien définie par une horloge. L’amplitude (A) du signal au moment du top de l’horloge est prise comme référence pour cette tranche. C’est cette valeur qui sera codée.
Si le signal est échantillonné à une fréquence de 100 Hertz (exemple), chaque tranche de temps, appelée période, est égale à 1/100 = 0,01 seconde, soit 10 millisecondes.
La fréquence d’échantillonnage (sampling rate) doit être suffisamment grande pour restituer intégralement le signal. Le théorème de Nyquist-Shannon dit que, pour respecter le signal-source, cette fréquence doit être au moins le double de celle de la plus grande fréquence possible dans le signal à échantillonner.![]() Codage
Codage- Cette étape consiste à peser l’amplitude A du signal en termes d’amplitudes élémentaires, chacune correspondant à un poids binaire (4, 2, 1). Autrement-dit, on opère une conversion du nombre décimal en volts (Adécimal = 7 volts) en un mot binaire (Abinaire = 0111).
- Le signal analogique est transformé en une suite de mots binaires. Ici: 100, 110, 111, 110, …
- Dans le cas d’une transmission, au lieu de transmettre un signal continu, le système devra transmettre une suite de mots binaires selon un format adapté, un protocole.
- Protocole: ensemble de règles permettant à deux ou plusieurs ordinateurs d’un réseau de communiquer entre eux. Internet utilise, entre autres, les protocoles TCP et IP afin de permettre la transmission d’informations d’une machine à une autre.
 Le théorème de Nyquist-Shannon dit que, pour respecter le signal-source, cette fréquence doit être au moins le double de celle de la plus grande fréquence rencontrée dans le signal à échantillonner. Un tel échantillonnage permet en théorie une reconstruction parfaite du signal-source. Pour la musique, dont l’oreille ne perçoit pas les fréquences au-delà de 22 kHz (pour être large), une fréquence d’échantillonnage de 44 kHz est en théorie suffisante. La fréquence d’échantillonnage d’un CD audio est normalisée à 44,1 kHz. Pour le téléphone, la voix ne nécessite que 4 kHz et un échantillonnage à 8 kHz est suffisant. Le téléphone, à travers ses composants numériques, ne passera pas votre musique préférée; tout ce qui est au-dessus de 4 kHz sera supprimé.
Le théorème de Nyquist-Shannon dit que, pour respecter le signal-source, cette fréquence doit être au moins le double de celle de la plus grande fréquence rencontrée dans le signal à échantillonner. Un tel échantillonnage permet en théorie une reconstruction parfaite du signal-source. Pour la musique, dont l’oreille ne perçoit pas les fréquences au-delà de 22 kHz (pour être large), une fréquence d’échantillonnage de 44 kHz est en théorie suffisante. La fréquence d’échantillonnage d’un CD audio est normalisée à 44,1 kHz. Pour le téléphone, la voix ne nécessite que 4 kHz et un échantillonnage à 8 kHz est suffisant. Le téléphone, à travers ses composants numériques, ne passera pas votre musique préférée; tout ce qui est au-dessus de 4 kHz sera supprimé.
il obtient une licence de mathématiques et de physique. Il entre au M.I.T et dans sa thèse de Master, « Une analyse symbolique des circuit à relais et de commutation » il utilise l’algèbre de Boole pour concevoir les circuits de commutation. Il apporte ainsi un outil théorique aux concepteurs de circuits logiques, qui servira aussi bien pour les circuits à relais que pour les circuits intégrés. Le professeur Howard Gardner de Harward considère cette thèse comme peut – être la plus importante du siècle. Il travaille en même temps sur l’analyseur différentiel de Vannevar Bush.
 Il publie en 1949 « Théorie de la communication des systèmes secrets ».C’est dans le cadre de ses travaux à la Bell qu’il publie, également en 1949, aidé du mathématicien Waren Weaver, le texte fondateur de la théorie de l’information, son fameux « Théorie mathématique de la communication »C’est aussi en 1949 qu’il épouse Mary Elisabeth « Betty » Moore qui lui donnera 3 enfants.
Il publie en 1949 « Théorie de la communication des systèmes secrets ».C’est dans le cadre de ses travaux à la Bell qu’il publie, également en 1949, aidé du mathématicien Waren Weaver, le texte fondateur de la théorie de l’information, son fameux « Théorie mathématique de la communication »C’est aussi en 1949 qu’il épouse Mary Elisabeth « Betty » Moore qui lui donnera 3 enfants.
Claude Shannon est par ailleurs un esprit curieux de tout. Il fabrique une machines à jongler, une souris qui traverse les labyrinthes, une machine qui résout le cube de Rubik, une autre qui joue aux échecs, qui ne sera battue qu’en 42 coups par le champion du monde Mikhail Botvinnik en 1965 à Moscou. Cela ne l’empêche pas de recevoir toutes les distinctions que son génie mérite, en particulier la Médaille Nationale de la Science des mains du président Johnson en 1966 et le Prix Kyoto pour la Science de Base.
Il était membre de nombreuses et prestigieuses sociétés savants et docteur Honoris Causa de nombreuses universités : Yale, Michigan, Princeton, Edimburgh, Princeton, Pittsburgh, Northwestern, Oxford, East Anglia, Carnegie-Mellon, Tufts, Pennsylvania. Même après sa retraite de professeur, il continuera à travailler au MIT jusqu’à ce que la maladie d’Alzeimer le conduise au Courtyard Nursing Care Center de Medford, Mass. où il mourra le 24 février 2001.
L’importance des travaux de Shannon
La présentation par Claude Shannon dans les années 1940 de la théorie de l’information est certainement une des grandes réalisations du XX° siècle. La théorie de l’information a eu grande influence sur les mathématiques en particulier sur la théorie des probabilités, et les mathématiques de Shannon en elles mêmes sont une contribution importante aux mathématiques pures. Dans son papier maintenant classique il a formulé un modèle de système de communication remarquable par sa généralité et sa facilité à être traité mathématiquement. Il a formulé les problèmes théoriques centraux et leur a donné une solution élégante. L’idée de base est que tout message se résume à une suite de 0 et de 1. On peut en effet digitaliser tout signal sans perte d’information pourvu que la fréquence d’échantillonnage soit supérieure au double de plus haute fréquence à transmettre (Théorème de Shannon).

Shannon voit le processus de communication comme stochastique par nature. L’aspect sémantique de l’information ne joue aucun rôle dans son modèle. L’information d’une « source », définie comme un processus stochastique doit être transmise par un « canal » défini par une loi de probabilité de transition reliant entrée et sortie de celui-ci. Le concepteur du système peut placer un codeur entre source et canal qui peut introduire un retard fixe et fini, et un décodeur entre canal et sortie. Sa théorie cherche à répondre à des questions telles que la rapidité et la fiabilité de la transmission, en optimisant codeur et décodeur. Shannon donne des réponses élégantes à ces questions. Sa solution comprend deux parties :
- La 1ère donne des limites fondamentales, par exemple que pour une source et un canal donnés il est impossible d’obtenir une fidélité et une fiabilité supérieures à des valeurs données.
- La 2ème montre qu’on peut atteindre la limite théorique moyennant un codeur pouvant apporter un retard important. Pour ce faire ce codeur peut utiliser un code complexe, pas nécessairement implémentable en pratique.
Un de ses apports les plus importants a été de montrer qu’on pouvait étudier source et canal indépendamment, en supposant qu’ils étaient connectés par une interface digitale. On définira le codeur pour optimiser la performance source/canal et le décodeur pour optimiser le canal comme transmetteur digital. La résolution des problèmes de la source et du canal résout de facto celui de la liaison complète. La complexification des systèmes informatiques et de communication rend de plus en plus nécessaires les apports théoriques de Shannon qui débordent même la pure technique pour apporter des outils déterminants dans des sciences humaines telles que la linguistique.
Consulter le texte original de Shannon
A ne pas lire…
Sahih
![]() Les critères pour qu’on reste amis sont simples et se résument en la foi dans les valeurs de la charte universelle des droits de l’Homme. Si quelqu’un y voit une objection, désolé, il devra quitter mon univers. A ceux-là je dirai:
Les critères pour qu’on reste amis sont simples et se résument en la foi dans les valeurs de la charte universelle des droits de l’Homme. Si quelqu’un y voit une objection, désolé, il devra quitter mon univers. A ceux-là je dirai:
Vous invoquez Dieu, j’invoque l’Amour et tous les deux, Dieu et Amour, comme par hasard, personne ne les a vus et pourtant on y croit. Tout est dans la foi, cette conviction profonde qui fait que nous en faisons un argument pour nous obliger à rester, pour les uns, dans le droit chemin, pour les autres, dans le respect des autres. Ma conviction est préférable car l’humain, pour certains, une créature de Dieu, pour moi, est bien réel. Ma relation avec l’au delà, qu’est-ce qu’elle m’importe ? Personne ne peut me dire à quoi cela ressemble. Et, puisque on s’y prépare au présent, je me contente d’en faire l’exemple du partage et du respect.
Si le beau qui est en moi rencontre le beau qu’on nous promet dans l’au delà, j’aurai réussi à faire ma vie, à ma manière tout en ne ratant pas la récompense suprême: être aimé ici bas pour mériter leur paradis sans m’obliger à des contorsions auxquelles je ne comprends rien. Aimez-vous, les uns les autres dira le prophète chrétien et le prophète musulman d’ajouter: « préfère aux autres ce que tu préfères pour toi ! » Le paradis dont on nous parle n’est une invention de l’esprit que dans la tête de ceux qui ne comprennent pas que c’est dans l’Amour que Dieu réside et non dans la bave qui accompagne les discours de haine et de division.
Science Vs Religion

Table des matières


 Codage
Codage
